TLA+哲学家问题~

希望这是最后一次开坑TLA+，期望至少学点东西，也能够分享点东西出来

哲学家问题

简单回顾下Dijkstra提出的哲学家问题，5个哲学家坐在圆桌前，两个哲学家之间有一把叉子，哲学家有三个状态：

  1. 思考：思考累了就会饿
  2. 饿了：饿了就会想吃饭，吃饭前提是需要同时把左右两侧的叉子都拿到，每把叉子同时只能被一个哲学家使用
  3. 吃饭：吃饱了就会放下叉子以供其他人使用，重新开始思考

一个哲学家问题的解决方案要满足如下两个条件

  1. safety: 一个正在吃饭的哲学家两侧的哲学家不能在同时吃饭（因为叉子不能共享）
  2. liveness: 没有哲学家会挨饿，也就是有限时间内饿了的哲学家都能吃上饭

遗憾的是……今天这个文里面无法解决liveness

废话几句

关于TLA+或者PlusCal这里都不会详细介绍，它们的困难主要在于：

  1. 几乎只有英文资料，想找到合适的学习资料也汉南，学习曲线极其陡峭

    这已经是我至少第三次尝试开坑

  2. 语法和概念纷繁错杂，这两个东西语法有所关联，且极其容易混淆
  3. 就算看懂了语法，想要真正动手写出来，难度相当离谱

这篇文章里都是直接用PlusCal来实现算法，由toolbox来翻译为TLA+，因此在类似伪代码的PlusCal部分会有相应的注释，但不会介绍语法以及TLA+ Toolbox怎么使用。

语法可能适合单独开坑，否则真的太难

简单实现

我们把问题抽象一下以方便实现：

  1. 总共有N个哲学家，N把叉子，都是zero-indexed，我们在实际运行的时候N取3
  2. 每把叉子都有一个状态（用一个数字表示）
    1. 如果是N表示没有哲学家持有这把叉子
    2. 如果不是N，那就是对应下表的哲学家持有这把叉子
  3. 哲学家有三个状态：Thinking Hungry Eating
\* 叉子和哲学家都是0-indexed
\* 总共有N个叉子和哲学家 所有叉子一开始的持有者都为N 也就是没有人持有
variable
    fork = [k \in Procs |-> N],
    state = [k \in Procs |-> "Thinking"];

然后我们定义一些辅助函数，用来获取左右两侧的叉子和哲学家的下标，以及我们希望TLC去检查的Invariant。这个Invariant在验证的每个状态中都会去验证，也就是开头说的safety，我这里命名成OnlyICanEat。

define
    \* 第i个fork是否可以使用
    Available(i) == fork[i] = N
    \* 第i个哲学家左边的叉子序号
    LeftF(i) == i
    \* 第i个哲学家左边的哲学家序号
    LeftP(i) == IF i = 0 THEN N - 1 ELSE i - 1
    \* 第i个哲学家右边的叉子序号
    RightF(i) == IF i = N - 1 THEN 0 ELSE i + 1
    RightP(i) == IF i = N - 1 THEN 0 ELSE i + 1

    \* Invariant: 如果一个哲学家正在吃饭 他左边或者右边的哲学家都不能在吃饭
    \* 另外如果所有都不满足条件 \A也为真
    OnlyICanEat ==
        \A p \in Procs:
            state[p] = "Eating" =>
                (state[LeftP(p)] /= "Eating" /\ state[RightP(p)] /= "Eating")
end define;

好了到这里开始真的实现算法：

  1. 如果是Thinking，那就会转成Hungry。
  2. 如果是Hungry，先去拿右手叉子，再拿左手叉子，然后转成Eating。await会一直阻塞直到条件成立，可以参考注释。
  3. 如果是Eating，放下左右手叉子，转成Thinking。
\* 总共有Procs个哲学家 每个process都有一个变量self是自己在Procs的下标
fair process Philosopher \in Procs
begin
Dinner:
    while (TRUE) do
        either T2H:
            if state[self] = "Thinking" then
                state[self] := "Hungry";
            end if;
        or GrabFork:
            \* 因为都会先拿右手叉子 再拿左手叉子 就会死锁
            if state[self] = "Hungry" then
            GrabRightFork:
                \* RightF(self)获取右手叉子下标
                \* Available(RightF(self))会返回右手叉子能否使用
                await(Available(RightF(self)));
                fork[RightF(self)] := self;
            GrabLeftFork:
                \* 等待左手叉子能被self使用
                await(Available(LeftF(self)));
                fork[LeftF(self)] := self;
                state[self] := "Eating";
            end if;
        or E2T:
            if state[self] = "Eating" then
                state[self] := "Thinking";
                \* 同时放下左边叉子和右边叉子
                fork[LeftF(self)] := N || fork[RightF(self)] := N;
            end if;
        end either;
    end while;
end process;

显然因为所有哲学家都先拿右手叉子，再拿左手叉子，会出现所有哲学家都拿了右手叉子，而都在等待左手叉子的情况，这里出现了循环等待的情况，导致出现了死锁的状况。

我们在TLC中可以看到最终的三个进程都卡在GrabLeftFork这一步，然后fork这里表示0, 1, 2这三把叉子分别被2, 1, 0这三个Hungry状态的哲学家所持有的。

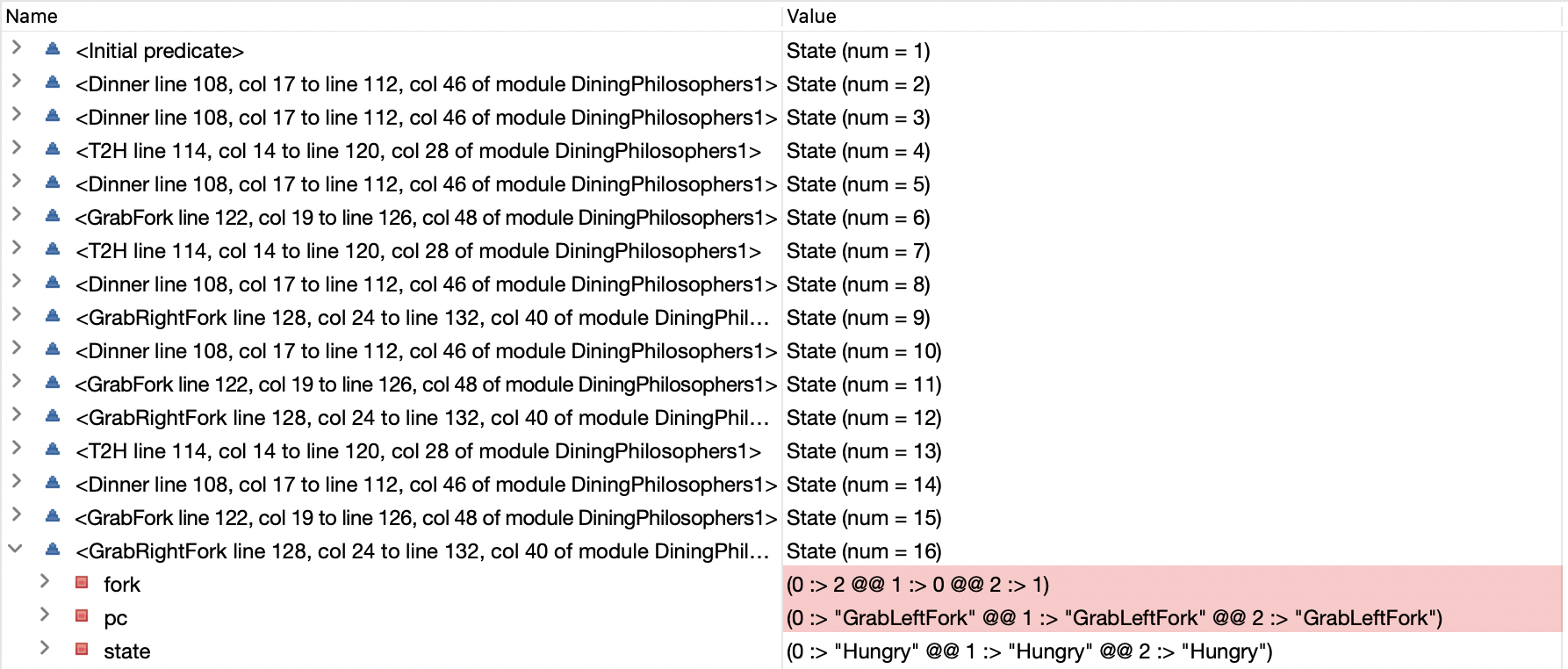
figure

完整实现如下

---------------- MODULE DiningPhilosophers1 ----------------
EXTENDS Naturals
CONSTANT N
ASSUME N \in Nat
Procs == 0..N-1

(*--algorithm DiningPhilosopher

\* 叉子和哲学家都是0-indexed
\* 总共有N个叉子和哲学家 所有叉子一开始的持有者都为N 也就是没有人持有
variable
    fork = [k \in Procs |-> N],
    state = [k \in Procs |-> "Thinking"];

(*
假设5个哲学家 5把叉子 P代表哲学家 F代表叉子
F0 P0 F1 P1 F2 P2 F3 P3 F4 P4 [F0 P0 ... ]
*)

define
    \* 第i个fork是否可以使用
    Available(i) == fork[i] = N
    \* 第i个哲学家左边的叉子序号
    LeftF(i) == i
    \* 第i个哲学家左边的哲学家序号
    LeftP(i) == IF i = 0 THEN N - 1 ELSE i - 1
    \* 第i个哲学家右边的叉子序号
    RightF(i) == IF i = N - 1 THEN 0 ELSE i + 1
    RightP(i) == IF i = N - 1 THEN 0 ELSE i + 1

    \* Invariant: 如果一个哲学家正在吃饭 他左边或者右边的哲学家都不能在吃饭
    \* 另外如果所有都不满足条件 \A也为真
    OnlyICanEat ==
        \A p \in Procs:
            state[p] = "Eating" =>
                (state[LeftP(p)] /= "Eating" /\ state[RightP(p)] /= "Eating")
    \* Temporal property: 哲学家不能被饿死 因为算法不够fair 还无法通过
    (*
    NoStarvation ==
        \* [] means always
        \* <> means eventually
        \* 连起来就是如果某个哲学家的状态是Hungry 它迟早一定会吃上饭
        \A p \in Procs: []((state[p] = "Hungry") => <>(state[p] = "Eating"))
    *)
end define;

fair process Philosopher \in Procs
begin
Dinner:
    while (TRUE) do
        either T2H:
            if state[self] = "Thinking" then
                state[self] := "Hungry";
            end if;
        or GrabFork:
            if state[self] = "Hungry" then
            GrabRightFork:
                await(Available(RightF(self)));
                fork[RightF(self)] := self;
            GrabLeftFork:
                await(Available(LeftF(self)));
                fork[LeftF(self)] := self;
                state[self] := "Eating";
            end if;
        or E2T:
            if state[self] = "Eating" then
                state[self] := "Thinking";
                fork[LeftF(self)] := N || fork[RightF(self)] := N;
            end if;
        end either;
    end while;
end process;
end algorithm; *)
===========================================================

一个看似正确的实现

一种很简单的修改方法是，让所有哲学家不要都先拿右手叉子，再拿左手叉子。我这里就让第0个哲学家先拿左手再拿右手叉子，其余都先拿右手再拿左手叉子。这样的不对称获取资源的顺序，实际上是打破了死锁的一个必要条件: 循环依赖。

fair process Philosopher \in Procs
begin
Dinner:
    while (TRUE) do
        either T2H:
            if state[self] = "Thinking" then
                state[self] := "Hungry";
            end if;
        or GrabFork:
            \* 第0个哲学家先拿左手再拿右手叉子 其余都先拿右手再拿左手
            \* 这样的不对称获取资源的顺序 实际上是打破了死锁的一个必要条件: 循环依赖
            if self = 0 /\ state[self] = "Hungry" then
                await(Available(LeftF(self)));
                fork[LeftF(self)] := self;
            GrabTheOtherDifferently:
                await(Available(RightF(self)));
                fork[RightF(self)] := self;
                state[self] := "Eating";
            elsif self /= 0 /\ state[self] = "Hungry" then
                await(Available(RightF(self)));
                fork[RightF(self)] := self;
            GrabTheOther:
                await(Available(LeftF(self)));
                fork[LeftF(self)] := self;
                state[self] := "Eating";
            else
                skip;
            end if;
        or E2T:
            if state[self] = "Eating" then
                state[self] := "Thinking";
                fork[LeftF(self)] := N || fork[RightF(self)] := N;
            end if;
        end either;
    end while;
end process;

这时候如果我们只检查OnlyICanEat这个Invariant，是能通过TLC检查的。

如何让哲学家不挨饿

然而上面的实现只能满足safety，而不能满足liveness。我们把哲学家不能挨饿这个Temporal Property加上：

    \* Temporal property: 哲学家不能被饿死 因为算法不够fair 还无法通过
    NoStarvation ==
        \* [] means always
        \* <> means sometime in the future
        \* 连起来就是如果某个哲学家的状态是Hungry 它迟早一定会吃上饭
        \A p \in Procs: []((state[p] = "Hungry") => <>(state[p] = "Eating"))

我们再次运行，会提示我们Temporal properties were violated。我们来看看发生了啥：

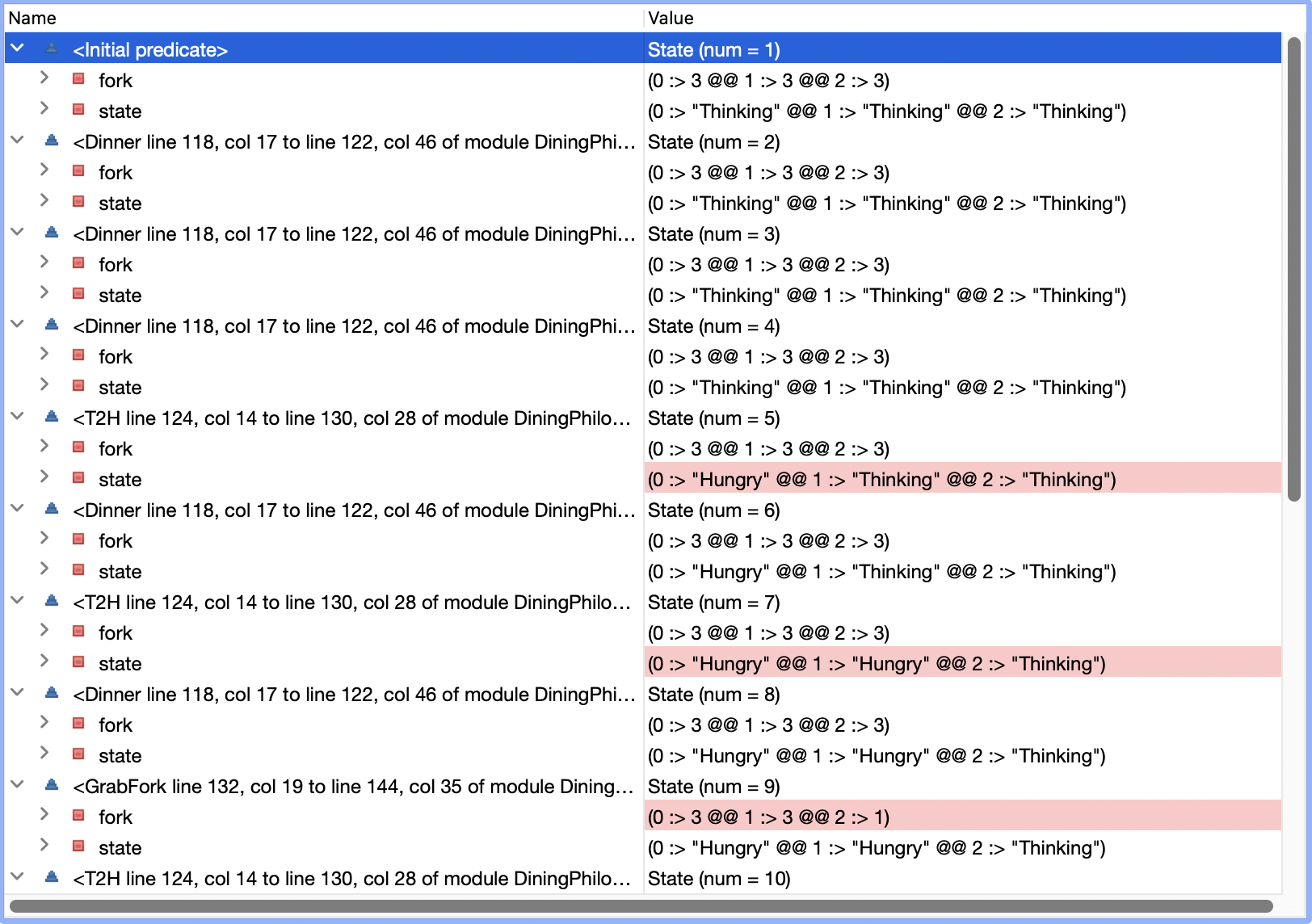
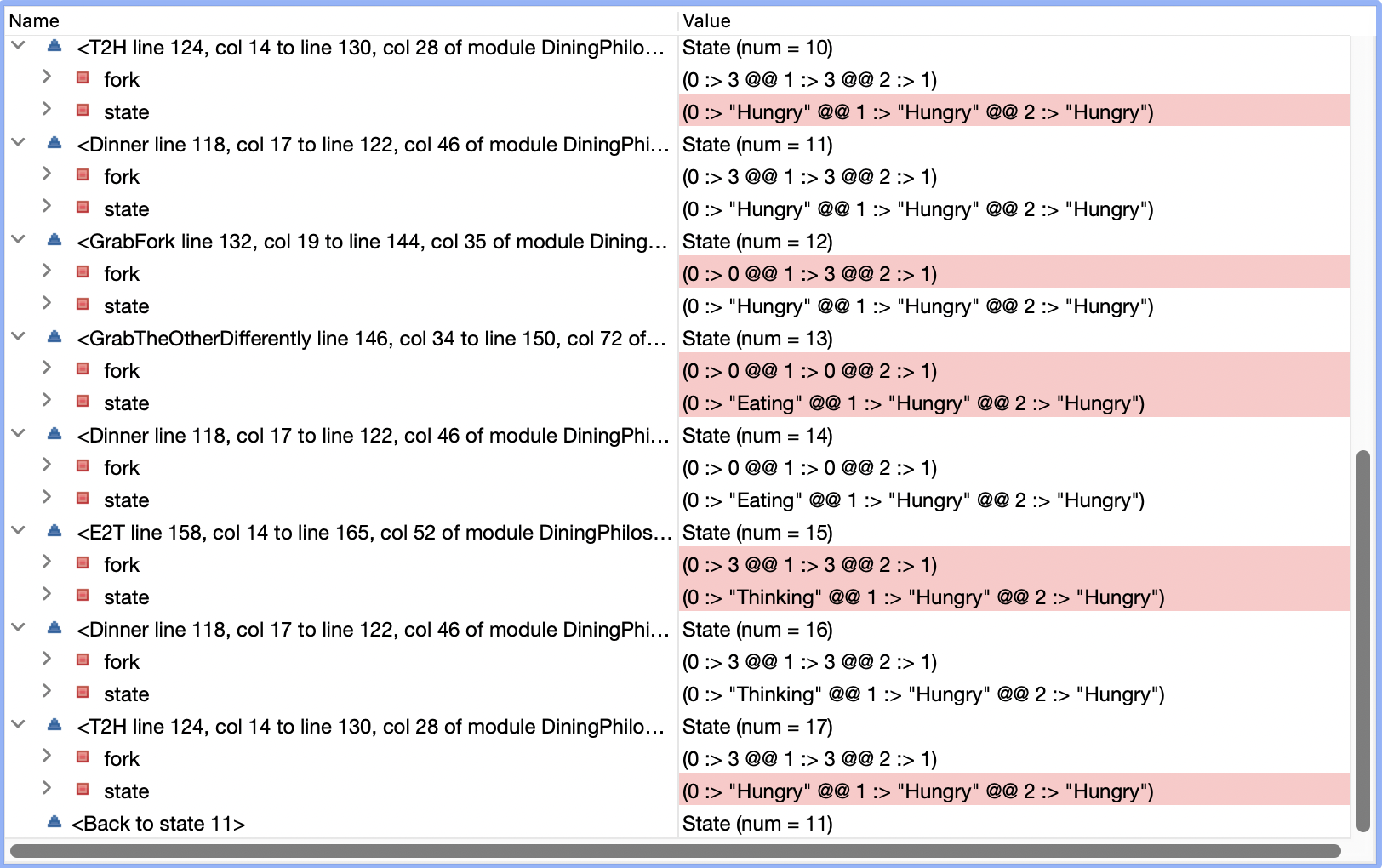
figure

figure

不得不吐槽一下Toolbox在显示上很难用

总共有1 - 17这么多状态，在最后提示Back to state 11，出现了循环，我们大概看下发生了啥。

  1. 在State(num = 10)的时候，三个哲学家都处于Hungry状态，且只有第2个叉子被第1个哲学家持有
  2. 在State(num = 12)的时候，三个哲学家都处于Hungry状态，第2个叉子被第1个哲学家持有（还想获取第1个叉子），并且第0个叉子被第0个哲学家持有
  3. 在State(num = 13)的时候，第0个哲学家同时拿到了左右两个叉子开始吃饭
  4. 在State(num = 15)的时候，第0个哲学家吃完了把两侧叉子都放下了，此时第2个叉子仍然被第1个哲学家持有（他已经饿了很久了）
  5. 最后又回到了State(num = 11)，也就是11-17这些状态可以无限循环，导致第1个哲学家在获取了右手叉子后，由于第0个哲学家不断重复饥饿 → 获取第0个和第1个叉子 → 吃饭 → 放下叉子 → 饥饿这个循环，导致我们可敬的第1个哲学家永远只能拿着第2个叉子干看着，最后饿死了。

我们该怎么办

首先，出现liveness的问题有几点：

  • fairness

我们在代码中写的是fair process，这在TLA+中是一个一个weakly fairness模型，其定义是A weakly fair action will, if it stays enabled, eventually happen. 在上面的例子中，被饿死的哲学家一直在等左手的叉子，这个叉子不断在被其他哲学家获取又释放。实际被饿死的哲学家是有机会能得到这个叉子的，但是所谓weakly fairness要求一个label必须stay enabled才是合法（合法代表TLC可以选择这个label下一个执行），左手叉子不断重复可用 → 不可用 → 不可用 → 可用 ...这个不是stay enabled，所以才会出现liveness问题。 要解决这个问题的办法就是改成strongly fariness模型，也就是代码中写成fair+ process，其定义是A strongly fair action, if it’s repeatedly enabled, will eventually happen. 也就是一个label不需要stay enabled，不断被enable → disable → enable的label也是合法的，因此在strongly fairness下不会出现饿死的情况。

  • 这个模型本身会导致liveness

上面说的fairness是TLA+中的概念，而现实世界中，由于线程调度，cpu时间分片，各种同步机制实现等等原因，对特定的哲学家，不能保证在有限时间内从Hungry变成Eating状态，是完全可能出现上面所说的某个哲学家被饿死的情况的。

解决模型本身的问题相当复杂，可以参考这个论文，The Drinking Philosophers Problem，有时间我争取写(抄)一下这个算法的实现再分享。

You May Also Enjoy

Coroutine internals

上次研究了Fiber，这次结合C++ Coroutines TS(N4680)和folly::coro::Baton，看看Coroutine~

Jemalloc 5.3.0 internals, part 3

上一篇介绍了hpa (huge page allocator)，这一篇继续介绍物理层的另一种page allocator: pac (page allocator classic)。