Drinking philosophers in TLA+

July 18, 2022

TLA+进阶哲学家问题~

我们在上一篇大概介绍了如何通过TLA+来验证哲学家问题。一个哲学家问题的解法要能满足如下两个性质：

safety: 一个正在吃饭的哲学家两侧的哲学家不能在同时吃饭（因为叉子不能共享）
liveness（或者叫fairness）: 没有哲学家会挨饿，也就是有限时间内饿了的哲学家都能吃上饭

在之前的模型下，我们只能保证safety，而不能保证liveness。这篇文章我们会详细探讨一下为什么之前的解法不能解决liveness，以及从Dining philosopher问题引出来的另一篇经典论文The Drinking Philosophers Problem。

一些基础

哲学家问题，又或者分布式系统经常会遇到的问题就是如何解决不同进程同时想要获取同一个资源。如果发生冲突的多个进程的所有属性都相同，我们就没有办法从这些冲突进程中按照某种规则挑出一个，在这种情况下就只能随机挑选一个，此时就变成了一个概率算法。

而如果我们想要一个确定的算法，从冲突进程中挑选一个的某种规则就至关重要，这个规则需要满足两个关键性质：

Distinguishability. In every state of the system at least one process in every set of conflicting processes must be distinguishable from the other processes of the set.

也就是要有一个性质能够挑选出特定process，最简单就是process id
Fairness. Fairness requires that the states that obtain when conflicts occur not always be identical.

也就是对于同样的冲突进程，不能总是选择同一个作为最高优先级，否则就会用公平性问题。

多个进程的优先级

为了检验冲突进程挑选规则能否满足Distinguishability和Fairness，论文里面引入了一个有向图，其中点用来表示各个进程，然后进程u到v之间的边E(u, v)代表两个进程之间可能会有冲突，且边的起点比终点拥有更高优先级。所以如下图的一个有向图说明优先级排序为p > q > r。

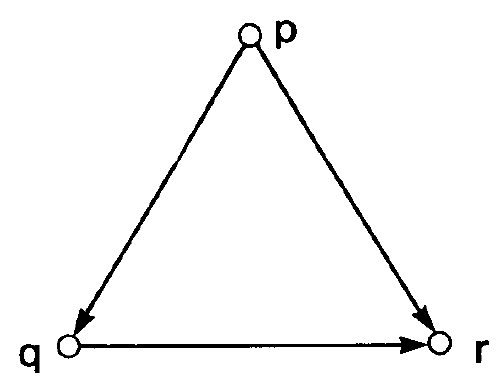
另外定义了p的depth为从任意一个入度为0进程开始，到p经过的最多的边数。所以

depth(p) = 0
depth(q) = 1
depth(r) = 2

显然，为了能够满足Distinguishability，这个有向图中不能出现环。而为了满足Fairness，在常数时间之内，任意进程p在的这个有向图中的depth要能变为0（或者说入度为0）。那改变这个有向图要满足如下性质（其实唯一能做的就是改变边的方向）：

Acyclicity Rule. All edges incident on a process p may be simultaneously (i.e., in one atomic action) redirected toward p.
Fairness Rule. Within finite time after a conflict is resolved in favor of a process p at depth 0, p must yield precedence to all its neighbors.

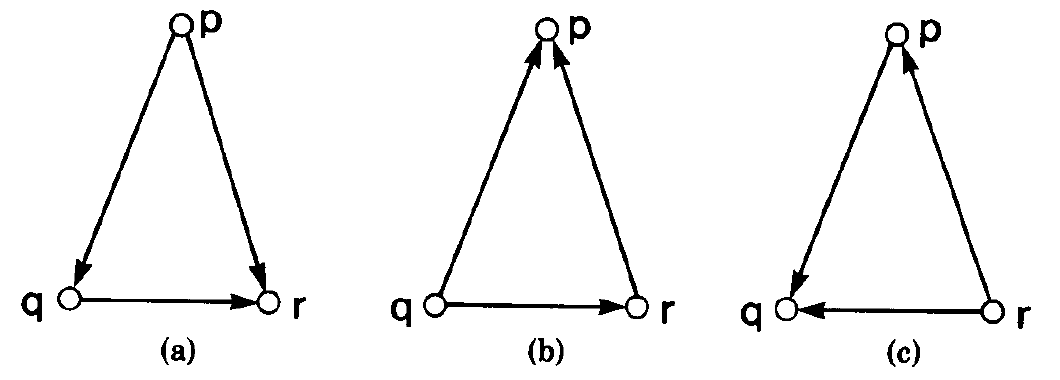
论文里举的例子就是通过切换某个进程的所有边的方向，上图中的三个进程的入度可以变为0，即拥有最高优先级。(比如a → b是切换了p的两条边方向，b → c是切换了q的两条边方向）

Drinking philosopher

论文其实在Dining philosopher问题的基础上又抽象出了一个更通用的Drinking philosopher问题，为了避免混乱，我们都统一用Dining philosopher问题中的术语，即哲学家、叉子、吃饭等。

我们回顾下之前的哲学家问题解决办法，先拿到叉子的哲学家在吃饭之前，永远不会释放叉子这个资源。如果所有哲学家都先拿右手叉子，而在等待左手叉子，对于某个叉子同时都有两个哲学家想要使用，我们光靠叉子没有办法区分出来某个哲学家更优于另一个哲学家。

因此想要满足liveness，我们需要引入一些额外的资源来标识哲学家的优先级。引入额外资源来标识优先级的作用主要是哲学家在适当的时候，可以放弃已经获取到的叉子。这个算法中唯一引入的额外资源就是叉子的状态，算法的核心思想可以用以下两点来概括：

叉子可以是干净的或者是脏的。叉子在哲学家吃饭的时候会从干净的变成脏的，而只有在下面说的从一个哲学家转交给另一个哲学家的过程中才会从脏的变成干净的，其余时候都不会改变状态。
如果某个哲学家已经获取了干净的叉子，就不会放弃这个叉子。而如果哲学家获取了一个脏的叉子，此时其他哲学家想要获取这个脏的叉子，就可以把它变成干净的叉子，并转交出去。

收到这个叉子的哲学家就不会再转交了，因为叉子已经变成了干净的叉子

第2点实际是算法的核心，它说明了什么时候哲学家需要放弃一个已经获取到的叉子。以下任意一个情形，都能说明哲学家u的优先级在高于哲学家v的优先级，此时在有向图中有一条u指向v的边：

case 1: 哲学家u拿着这把叉子，且叉子是干净的
case 2: 哲学家v拿着这把叉子，且叉子是脏的
case 3: 哲学家v把叉子递给了哲学家u

这三点都暗含在上面说的算法核心中，论文里证明了这个算法是能够满足前面说的各种性质。

Hygienic Dining Philosopher

由于叉子在传递前，哲学家会把脏的叉子变成干净的叉子，所以叫做干净的吃饭的哲学家。。。我们来看下算法实现。为了简化实现放弃和传递叉子的这个步骤，每把叉子都有一个request token，只有持有token的哲学家，才能要求获取这把叉子。

下面是放弃和传递叉子需要满足的条件和相应需要执行的动作，这些步骤都会在TLA+的实现中体现：

Hungry、持有token、不持有叉子f：此时就可以发送token要求获取这把叉子
不在Eating、持有token、持有脏叉子f：代表收到了其他哲学家发来的token要求获取这把叉子，此时应该释放叉子

然后看下初始值：

所有叉子必须都是脏的（如果都是干净的，就会出现死锁）
叉子和token必须持有在不同的哲学家手中，且叉子形成的优先级的有向图不能有环

然后分两部分说明这个算法为什么能成立

有向图永远不会出现环
1. 初始没有环
2. 传递叉子的操作也不会改变边的方向（只是修改了叉子的持有者以及从脏变干净），这一步不会导致有向图改变
3. 哲学家如果持有所有干净的叉子后，会把叉子都变成脏的，此时这个哲学家的所有边方向都取反了，这个操作根据前面的说明，也不会引入环

综上所述这个优先级的有向图永远不会出现环，所以当发生冲突时，总是能根据边的方向，挑选出优先级更高的哲学家，满足Distinguishability。

每个饥饿的哲学家最终都能吃上饭

假设u和v共享叉子，且u是饥饿的，分为几个情况：

u持有叉子，当u获取所有叉子都时候，就能吃饭
v持有叉子，又分成几种情况：
1. 叉子是脏的：
  - 如果u持有token，那么u就满足了R1的所有条件hungry、reqf(f), ~fork(f)，此时u会发送token给v，v在之后某个时间会持有token
  - 如果v持有token
  所以在叉子是脏的情况下，v在某个时间点一定会满足~eating、reqf(f)、dirty(f)，也就满足了R2的所有条件，此时v就会释放叉子，并转交一个干净的叉子给u
2. 叉子是干净的：
  
  持有这个叉子的哲学家一定是饥饿的。那么在有向图中有一条v → u的边，说明v优先级更高。当v吃完饭后，叉子就又变成了脏的，就会满足上面叉子是脏的那个路径。

TLA+实现

总共有N个哲学家，N把叉子，叉子的初始持有者保存在Topology中，token的初始持有者保存在RTopology中。根据paper中实现有几个初始条件：

所有叉子初始都是脏的
叉子和token的初始持有者不同

---------------- MODULE DiningPhilosophers6 ----------------
(* Dining philosophers problem, hygenic edition. *)
EXTENDS Naturals, TLC
CONSTANT N
ASSUME N \in Nat
Procs == 0..N-1
\* 总共有N个哲学家 N把叉子 N个token
\* fork优先级的初始值 set中的每个sequence的第一个元素拥有更高优先级
Topology == {<<0, 1>>, <<0, 2>>, <<1, 2>>}
\* request token优先级的初始值 set中的每个sequence的第一个元素拥有更高优先级
\* To simplify our description, we introduce a request token for each fork.
\* Only the holder of the request token for fork f can request fork f.
RTopology == {<<1, 0>>, <<2, 0>>, <<2, 1>>}

(*
1. A fork is either clean or dirty.
2. A fork being used to eat with is dirty and remains dirty until it is cleaned.
3. A clean fork remains clean until it is used for eating.
4. A philosopher cleans a fork when mailing it (he is hygienic).
5. A fork is cleaned only when it is mailed.
6. An eating philosopher does not satisfy requests for forks until he has finished eating.
*)

(*
--algorithm diningHygienic {
    variable
        \* initially forks are at lower id side of the edges
        \* 总共有三把叉子 <<0, 1>>, <<0, 2>>, <<1, 2>>, 持有者分别为0, 0, 1
        fork = Topology,
        \* initially none of the forks is clean
        \* 三把叉子都是脏的
        clean = {},
        \* initially req tokens are at higher id side of edges
        \* 总共有三个token <<1, 0>>, <<2, 0>>, <<2, 1>>, 持有者分别为1, 2, 2
        req = RTopology,
        state = [k \in Procs |-> "Thinking"];

    define {
        \* p, q两个哲学家之间是否共享fork
        Edge(p, q) == IF (<<p, q>> \in Topology \/ <<q, p>> \in Topology) THEN TRUE ELSE FALSE
        \* p的fork邻居
        GetNbrs(p) == {q \in Procs : Edge(p, q)}

        \* p和q是否共享fork 且fork持有者为p
        ForkAt(p, q) == IF (<<p, q>> \in fork) THEN TRUE ELSE FALSE
        \* p和q是否共享token 且token持有者为p
        ReqAt(p, q) == IF (<<p, q>> \in req) THEN TRUE ELSE FALSE
        \* p和q是否共享干净的fork
        Clean(p, q) == IF (<<p, q>> \in clean \/ <<q, p>> \in clean) THEN TRUE ELSE FALSE

        \* 找到p与其他人共享的fork，且满足以下条件: fork持有者不为p 但token持有者为p 也就是p可以给其他人发送token以要求这个fork
        ForksCanRequest(p) == {q \in Procs : Edge(p, q) /\ ~ForkAt(p, q) /\ ReqAt(p, q)}

        \* 找到p与其他人共享的fork，且满足以下条件: fork持有者为p token持有者也是为p 且fork是脏的(可以被其他人抢占)
        \* 这里需要注意的是没有办法区分token是由其他哲学家发送过来的 还是本来token就是由p持有
        \* 但无论那种情况 只要p不在吃饭且满足这些条件 这个fork对于p来说就可以释放
        ForksAreRequested(p) == {q \in Procs: Edge(p, q) /\ ReqAt(p, q) /\ ForkAt(p, q) /\ ~Clean(p, q)}

        \* Safety properties and liveness property to be checked
        OnlyICanEat == \A k,l \in Procs: (state[k] = "Eating" /\ state[l] = "Eating") => ~Edge(k,l)
        OneHoldFork == \A k,l \in Procs: ForkAt(k,l) => ~ForkAt(l,k)
        TheOtherHoldToken == \A k,l \in Procs: ReqAt(k,l) => ~ReqAt(l,k)
        NoStarvation == \A p \in Procs: [] (state[p] = "Hungry" => <> (state[p] = "Eating"))
    }

    fair process (j \in Procs)
    variable Q = {}, q = 0;
    {
    J0:
        while (TRUE) {
            \* The process checks if it needs to respond to any requests send to it for forks
            \* and does so if its state is not "Eating"
            \* 对应paper R2 command
            if (state[self] /= "Eating" /\ ForksAreRequested(self) /= {}) {
                \* gather the reqs for the dirty forks
                \* forks in Q are dirty, and must defer to others
                Q := ForksAreRequested(self);
            Ai:
                while (Q /= {}) {
                    q := CHOOSE k \in Q: TRUE;
                    Q := Q \ {q};
                    \* defer fork from self to q
                    \* so remove <<self, q>> and add <<q, self>>
                    fork := fork \ {<<self, q>>};
            Aii:
                    fork := fork \union {<<q, self>>};
                    \* clean the fork as sell
                    clean := clean \union {<<q, self>>};
                }
            }
            \* The process is hungry and has some forks to request, the process starts requesting its missing forks.
            \* 对应paper R1 command
            else if (state[self] = "Hungry" /\ ForksCanRequest(self) /= {}) {
                \* Q is the set of neighbors for which a fork needs to be requested.
                Q := ForksCanRequest(self);
            Hi:
                \* in each iteration of the loop, a neighbor is picked out from this set,
                \* and the request is sent to that neighbor's side.
                while (Q /= {}) {
                    q := CHOOSE k \in Q: TRUE;
                    Q := Q \ {q};
                    \* add the request token into req
                    req := req \ {<<self, q>>};
            Hii:
                    req := req \union {<<q, self>>};
                }
            }
            \* The process is "Hungry", and satisfies all the conditions to eat, it transitions to the "Eating" state.
            else if (state[self] = "Hungry" /\
                \* fork被self持有且(叉子干净，或者叉子虽然是脏的，但没有被其他人需求)
                    (\A k \in Procs: Edge(self, k) =>
                        ForkAt(self, k) /\ (Clean(self, k) \/ ~ReqAt(self, k)))) {
                \* In other words, a process can eat with some of the forks being dirty, provided that the corresponding
                \* neighbors for those dirty forks are not hungry and have not send requests for those forks.
                state[self] := "Eating";
            }
            else if (state[self] = "Eating") {
                state[self] := "Thinking";        \* if eating, go to thinking
                \* For this, the process marks all its forks as dirty, iterating over a while loop.
                Q := GetNbrs(self);
            Ei:
                while (Q /= {}) {
                    q := CHOOSE k \in Q: TRUE;
                    Q := Q \ {q};
                    clean := clean \ {<<self, q>>};
                }
            }
            else if (state[self] = "Thinking") {
                state[self] := "Hungry";
            }
        }
    }
}
============================================================

在define中定义了一些帮助函数，具体参见其中的注释。同时也写了几个operator用来检查这个模型能否满足safety和liveness：

OnlyICanEat用来检查如果某个哲学家在吃饭，与之共享叉子的哲学家不在吃饭
OneHoldFork和TheOtherHoldToken用来检查叉子和token不会同时被两个人持有
NoStarvation用来检查liveness：即如果有一个哲学家饿了，它在有限时间以内能吃上饭

从fair process开始是算法，Q用来保存从其他哲学家收到的token，q是个临时变量。几个分支分别用来处理：

如果没有在吃饭，且持有的脏叉子被其他哲学家需要，那么就会把叉子传递出去
如果饿了，且能够request叉子，那么就会发送token给持有脏叉子的哲学家
如果饿了，且持有所有叉子，那么开始吃饭
如果吃完饭了，就开始思考
如果思考累了，就有点饿了

核心的逻辑主要是在前两个分支，一个用于把叉子递给其他哲学家，一个用于去其他哲学家处要叉子。这个模型就能通过liveness检查，不过为了TLC运行占用的CPU和存储空间，当前模型是写死了只有3个哲学家，否则会出现运行几十分钟都无法搜索完所有状态空间的情况。

reference

Share on

Twitter Facebook LinkedIn

Drinking philosophers in TLA+

一些基础

多个进程的优先级

Drinking philosopher

Hygienic Dining Philosopher

TLA+实现

reference

Share on

You May Also Enjoy

Introduction to Aurora DSQL

Coroutine internals

folly::Fiber

Jemalloc 5.3.0 internals, part 3