Counting, Enumerating, and Sampling of Execution Plans in a Cost-Based Query Optimizer
最近补了一些优化器相关的背景知识,今天分享一篇论文Counting, Enumerating, and Sampling of Execution Plans in a Cost-Based Query Optimizer.pdf (sigmodrecord.org)。这个paper基于Volcano和Cascades优化器中的Memo数据结构,提出了一种对优化器生成的所有执行计划进行数量统计、枚举甚至采样的方法。优化器一般只会输出一个”最优“的执行计划,基于这种方法能够完成以下事情:
- 使用特定版本的执行计划运行
- 确定性的验证每个执行计划的正确性和性能
背景
很多优化器将优化分为两个阶段:
- 逻辑优化,这阶段会应用若干基于关系代数总是更优的规则,对逻辑计划进行等价替换。
- 物理优化,基于逻辑计划生成对应的物理计划,然后基于cost model进行物理优化。
Volcano/Cascades优化器中将逻辑优化和物理优化合并到了同一个阶段,但实际还是用了不同类型的规则,比如Transformation Rule对应逻辑优化,Implementation Rule对应物理优化。论文主要描述的方法,主要是在物理优化阶段使用Memo这个数据结构时,进行相应的处理。Memo主要用于管理多个Group,每个Group中的物理算子及其子树可以和同一个Group之内的其他算子及其算子进行替换。而优化器就是从这些等价替换中,挑选执行代价最小的一个执行计划。Memo的核心思想是通过尽可能的共用相同的子树使得内存的占用,以及搜索空间尽可能的小。
Memo的主要使用步骤如下:
- 初始化Memo
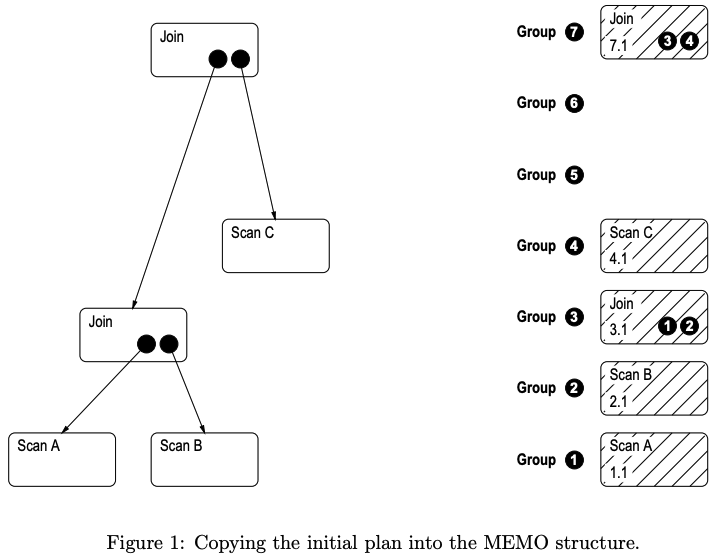
我们以下面这个执行计划为例,左侧是逻辑计划,我们基于逻辑计划可以初始化Memo如右图所示。每个Group中有若干算子,每个算子的左下角是算子的id,右下角则是算子的children所在的group。从Group 7中的每个算子触发,都可以构建出一个完整的逻辑或物理执行计划。
- 基于Memo进行规则匹配和转换
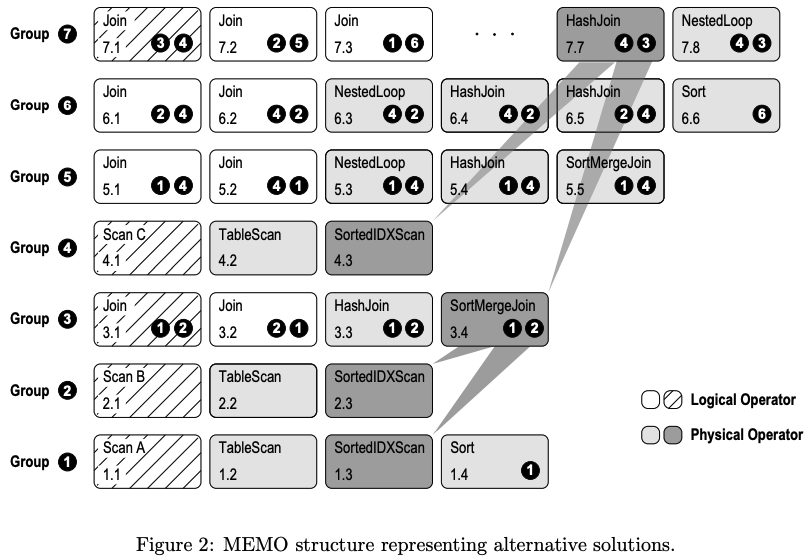
在初始化Memo完成之后,我们就可以基于逻辑算子,通过转换规则生成等价的其他算子。论文举了几个转换规则的例子:
- a logical operator in the same group, e.g.
join(A,B) -> join(B,A); - a physical operator in the same group, e.g.
join -> hash join; - a set of logical operators that form a connected subplan; the root goes to the original group, other operators may go to any group, including the creation of new groups as necessary, e.g.
join(A, join(B,C)) -> join(join(A,B), C).
比如如下是进行转换之后的Memo:
- 进行代价评估
对于每个执行计划,优化器都能够基于代价模型计算起运行代价,然后挑选一个”最优“的执行计划,交给执行器执行。
统计、枚举和采样执行计划
以上就是Volcano/Cascades优化器大概原理,当优化器把所有计划都生成之后,论文会基于这些计划进行数量统计,假设总共是N个计划,会给每个执行计划生成一个一一对应的id,映射到[0, N - 1]这个区间之内。基于这个id,也能够确定的还原出这棵执行计划树。同时有了这个数字之后,也能够基于这个数字,随机的挑选若干执行计划,达到枚举和采样的目的。我们看下实际的例子,假设经过优化器的若干优化后,最终输出Memo(Group 7中的两个算子作为根节点,并且把无关的逻辑算子和中间结果都取出后如下图所示)。
统计执行计划数量
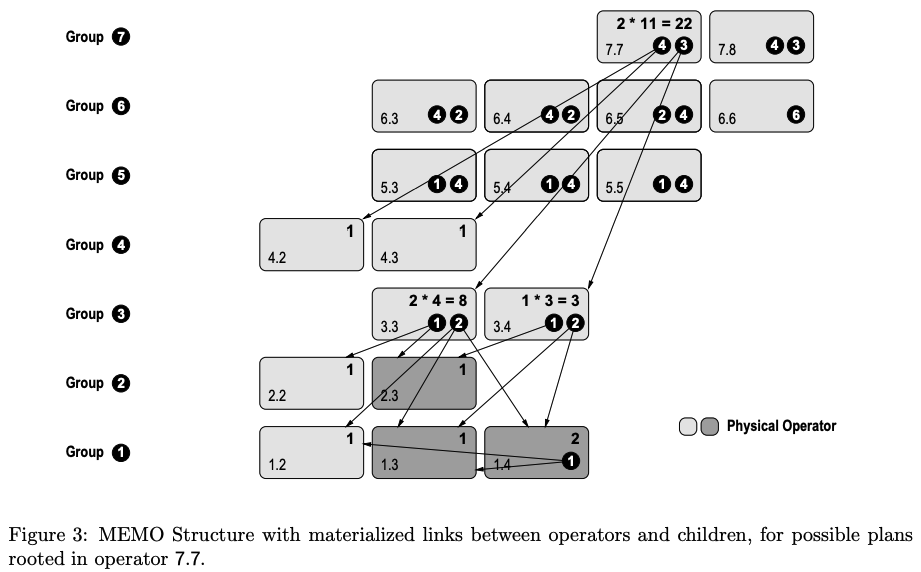
对于7.7为根节点的这个执行计划来说,总共有22种可能。这里的运算逻辑如下:
-
同一个operator内的多个children之间用乘法运算,如7.7中的2 * 11 = 22
每个children代表一个group,又比如3.3这个operator,其组合数就是由Group 1和Group 2的数量的乘积而得
-
同一个group之内的多个算子之间用加法运算,如Group 3中的3.3和3.4求和(8 + 3)就等于7.7中的Group 3的组合数11
而整个优化器输出的物理计划数量就是Root Group中的物理计划之和(即第二个规则)。当确定了执行计划的数量为N之后,就可以对所有执行计划进行编号(文中这个过程成为ranking)。编号对应的区间是[0, N - 1],编号和计划一一对应。通过编号就能进行随机选择和采样,或者选择特定的执行计划进行执行,比如文中给的例子

通过编号找到对应执行计划
从另一个角度看,给定任何一个rank,就能够唯一的确定相应的执行计划,这个过程文中称为unranking。两个核心规则如下:
- 在一个operator内需要对多个group进行选择时,采用求余和整除来计算各个group各自的sub-rank。
- 同一个group之内的选择,则可以直接根据rank在group之内的组合数的偏移量来决定。
对于同一个group之内,论文图中例子基本是二叉树,算法则是能拓展到多叉树的。只在operator3.3中是多叉。
我们以7.7这个root operator为例,总共有2 * 11 = 22中可能,zero-indexed:
- 比如给定rank = 17
- 在7.7中需要确定group 4和group 3的选择,应用规则1
- 对于group 4,左子树:17 % 2 = 1,所以group 4的sub-rank为1(其中2是group 4可能的组合数)
- 对于group 3,右子树:floor(17 / 2) = 8,所以group 3的sub-rank为8
- 7.7对应的group 4的operator有2种组合,应用规则2,选择下标为1的组合,即4.3
- 7.7对应的group 3的operator有11种组合,应用规则2,选择下标为8的组合,即选中了3.4作为下一步计算的根节点,3.4的sub-rank为(8 - 8) = 0。
- 在3.4中需要确定group 2和group 1的选择,应用规则1
- 对于group 2,左子树:0 % 1 = 0,所以group 2的sub-rank为0,最终也就选择了2.3
- 对于group 1,右子树:floor(0 / 1) = 0,所以group 1的sub-rank为0,最终选择1.3
所以最终17所代表的执行计划的先序遍历是:
7.7, 4.3, 3.4, 2.3, 1.3 - 在7.7中需要确定group 4和group 3的选择,应用规则1
- 又比如给定rank = 12
- 在7.7中需要确定group 4和group 3的选择,应用规则1
- 对于group 4,左子树:12 % 2 = 0,所以group 4的sub-rank为0
- 对于group 3,右子树:floor(12 / 2) =68,所以group 3的sub-rank为6
- 7.7对应的group 4的operator有2种组合,应用规则2,选择下标为0的组合,即4.2
- 7.7对应的group 3的operator有11种组合,应用规则2,选择下标为6的组合,即选中了3.3作为下一步计算的根节点,3.3的sub-rank为6。
- 在3.3中需要确定group 2和group 1的选择,应用规则1
- 对于group 2,左子树:6 % 2 = 0,所以group 2的sub-rank为0,最终也就选择了2.2
- 对于group 1,右子树:floor(6 / 2) = 3,所以group 1的sub-rank为3
- group 1的operator有四种组合,应用规则2,选择下标为3的组合,即选择1.4作为下一步计算的根节点,1.4的sub-rank为(3 - 1 - 1) = 1
- 1.4对应的group 1的operator有2种组合选择,应用规则2,选择下标为1的组合,即1.3
所以最终12所代表的的执行计划的先序遍历是:
7.7, 4.2, 3.3, 2.2, 1.4, 1.3 - 在7.7中需要确定group 4和group 3的选择,应用规则1
这一部分由于论文比较形式化和晦涩难懂,以上规则是我总结出来的,不排除理解错的可能。
结论
最后这篇论文还基于如上的算法,进行了实际的采样以及定量分析。个人理解这篇论文的优秀之处在于提供了一个确定性分析优化器输出结果的可能,对于优化器的可测性是有极大提升的,后续会研究下是否可以引入。