HyperLogLog in plain words

沉迷于优化器ing…

基数估计

想象我们有一个很大的带重复元素数据集, 无法全部放到内存中, 我们应该如何计算其不重复元素的个数呢? 如果需要精确值, 我们可以进行外排序之后, 再进行去重. 如果我们不需要精确值呢? 这也就是所谓的基数估计. 基数估计大量使用在数据库和计算框架中, 其主要目的都是在面对海量数据时, 用尽可能少的内存进行基数估计, 以供后续的分析和优化. 几个比较有名的基数估计算法有:

• Linear Counting
• LogLog
• HyperLogLog

这篇文章主要聚焦于后两个算法, 这些论文里面有大量的数学推导, 这篇文章试着用直白的语言简单说下背后的原理, 并结合示例和工程实现, 阐述算法背后的核心思想. 网上的介绍也很多, 文末也附上学习过程中参考的算法介绍, 感兴趣的可以看下.

Probabilistic counting

今天介绍的几个算法本身都是从Probabilistic counting衍生出来的, 三篇论文的链接如下:

Probabilistic Counting Algorithms for Data Base Applications

LogLog counting of large cardinalities

HyperLogLog: The analysis of a near-optimal cardinality estimation algorithm

LogLog和HyperLogLog都是基于概率统计的思想来进行基数估计的. 假设给定一个数, 用某个哈希函数得到一个哈希值, 其内部就是若干0和1组成的bitmap. 从统计的角度来说, 当生成的哈希值足够多时, 每一个哈希值中每一位是0或者1的概率都趋近于1/2.

基于这个想法, 给定任意一个哈希值, 其中出现连续k个0的几率就是1 / (2 ^ k). 换而言之, 每生成(2 ^ k)个哈希值, 就会期望其中有一个哈希值中, 有连续k个0. 基于这个想法, 一个朴素的基数估计算法就是: 统计原始数据的哈希值, 找到这些哈希值中, 最长连续出现了多少个0, 记为k, 最终估计基数为(2 ^ k).

这个算法的缺点在于, 由于只能给出2的整数次幂的估计, 它的随机偏差太大了. 但是优秀之处是, 它的空间占用非常小, 假设我们生成的哈希值是32位的, k的取值范围就是[0, 32], 只需要5个bit就可以表示这个范围. 第一个paper就是基于这个思想, 进行了更准确的估计, 这里就不展开说了.

一个优化方向就是, 使用多个哈希函数, 对每个哈希函数重复上面的过程中, 最终根据每个哈希函数的估计值, 求一个算术平均值作为最终估计结果. 这个算法的缺点在于计算哈希在这个过程中的开销太大了, 随着哈希函数的增多, 估计的时间会大大增加.

另一个优化方向则是仍然一个哈希函数, 但将生成的哈希值分段处理, 用哈希值的一部分来分片, 剩余部分用来进行连续k个0的统计. 比如对于一个32位哈希值, 我们用低10位作为分片下标, 总计有2 ^ 10 = 1024个bucket, 剩下的22位进行统计. 这其实就是LogLog算法的原型, 我们可以简单实现如下所示:

#include <iostream>
#include <random>
#include <vector>

using namespace std;

size_t trailingZeros(int32_t num) {
  if (num == 0) {
    return 32;
  }
  size_t count = 0;
  while ((num & 1) == 0) {
    num >>= 1;
    ++count;
  }
  return count;
}

/**
 * @brief Cardinality estimation based on LogLog algorithm
 *
 * @param values Values to be estimated
 * @param bucketExp The number of bits to represent as bucket number, there'll be (2 ^ bucketExp)
 * buckets
 * @return int32_t Estimated result
 */
float loglog(const std::vector<int32_t>& values, size_t bucketExp) {
  auto buckets = (1UL << bucketExp);
  std::vector<size_t> maxZeros(buckets, 0);
  for (const auto& value : values) {
    auto hashed = std::hash<int32_t>()(value);
    // get the index in (2 ^ bucketExp) buckets
    auto idx = hashed & (buckets - 1);
    // right shift and counting trailing zeros
    auto bucket_hash = hashed >> bucketExp;
    maxZeros[idx] = std::max(maxZeros[idx], trailingZeros(bucket_hash));
  }
  auto avgK = static_cast<float>(std::accumulate(maxZeros.begin(), maxZeros.end(), 0)) / buckets;
  // 0.79402 is a magic number given in paper
  return std::pow(2, avgK) * buckets * 0.79402;
}

void run() {
  std::uniform_int_distribution<> dist{std::numeric_limits<int32_t>::min(),
                                       std::numeric_limits<int32_t>::max()};
  std::random_device rd;
  std::default_random_engine rng{rd()};
  std::vector<int32_t> values;
  for (size_t i = 0; i < 10000; i++) {
    values.emplace_back(dist(rng));
  }
  std::sort(values.begin(), values.end());
  std::cout << "Estimated: " << loglog(values, 10)
            << ", Actual: " << std::unique(values.begin(), values.end()) - values.begin()
            << std::endl;
}

int main() {
    for (size_t i = 0; i < 10; i++) {
        run();
    }
}

可以看到整个代码非常简单, 我们总共进行10次基数估计, 每次基数估计生成10000个int32_t范围内的整数作为样本, 然后loglog函数负责进行基数估计. 其过程就是迭代每一个元素, 计算其哈希值, 求出bucket的下标, 然后根据最低位连续个0的个数, 到对应bucket中进行更新.

原始论文中是计算leading zeros, 这里为了方便, 改成了trailing zeros.

我们可以实际进行下基数估计, 看看这个算法的准确度咋样. 由于我生成的样本取值范围是int32_t的范围, 每次生成10000个, 因此几乎不可能出现重复元素, 下面运行结果的实际基数都是10000. 可以看到这个算法预估的基数其实非常接近实际结果了, 偏差实际在3% - 5%之间:

Estimated: 10306.8, Actual: 10000
Estimated: 10828.9, Actual: 10000
Estimated: 9684.53, Actual: 10000
Estimated: 10596.9, Actual: 10000
Estimated: 9625.71, Actual: 10000
Estimated: 10447.3, Actual: 10000
Estimated: 10133.9, Actual: 10000
Estimated: 10099.6, Actual: 10000
Estimated: 9970.56, Actual: 10000
Estimated: 10106.5, Actual: 10000

LogLog算法对于之前的朴素算法优化在于, 原先我们只能得到一个最长连续0的长度k, 而分成n个bucket之后, 我们就能得n个k, 最终求出算术平均数记为k’. 由于此时有n个bucket, 所以最终结果为n * (2 ^ k’). 上面代码中出现的系数0.79402则是论文中给出的一个经验系数. 而内存占用上, 如果假设总共1024个桶, 每个桶占用5bit, 则总计640字节. 论文中给出了LogLog估计的平均偏差率为: 1.3/sqrt(m), 其中m是bucket数量.

HyperLogLog

我们可以看到LogLog算法通过分片和算术平均数的引入, 提升了基数估计的准确率. 后面的研究又发现, 如果我们在求算术平均数时, 如果只计算[0 -70]%分位的结果时(也就是忽略最高的30%数据), 其准确率达到了1.05/sqrt(m), 这也就是所谓的SuperLogLog算法.

而后续的HyperLogLog算法则是使用了另外一种平均数: 调和平均数(倒数的算术平均数). 论文给出的准确率达到了1.04/sqrt(m). 当然实际的算法会比这里描述的复杂很多, 主要都是在处理当基数很小或者基数很大时的corner case, 感兴趣的可以读一下HyperLogLog的原始论文, 或者是google在工程化时引入的优化, 40671.pdf (googleusercontent.com).

HyerLogLog example

Sketch of the Day: HyperLogLog — Cornerstone of a Big Data Infrastructure – AK Tech Blog (neustar.biz)

我们可以在这个网站可视化的看到HyperLogLog的计算过程.

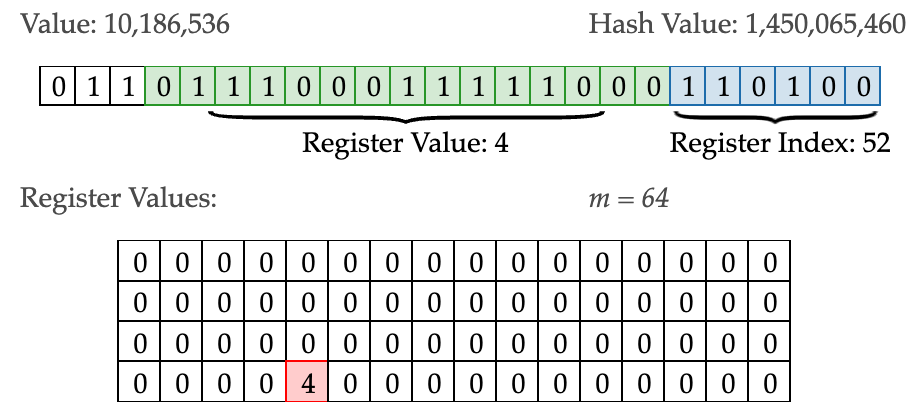
比如上图所示, 系统每次会生成一个24位的随机数, 计算其哈希值, 其中低6位(Register Index)用来表示桶的下标, 中间15位(Register Value)则用来基数统计, 高3位预留.

比如对于10186536, 计算Jenkins hash function, 得到哈希值为1450065460, 二进制表示如上所示. 其中:

• m 表示桶的个数, 分成了2 ^ 6 = 64个桶
• 蓝色的bit表示在桶中的下标, 例如图中的110100表示二进制的52，所以10186536被统计在中间大表格标红的第52个桶之中
• 绿色的bit用来做基数统计, 具体方式就是找到从右往左第一个1出现的位置, 记作当前这个value对应的Register Value：从图中可以看到标绿的bit中，从右往左数，第一个1出现在第4位，所以10186536对应的Register Value就是4, 将其更新到Register Values中的第52个桶中
• Register Values: 表格中的每一小格代表这个桶中, 目前遇到的最大的Register Value

这个网址可以根据指定每次生成的元素数量, 可视化的对比LogLog和HyperLogLog的误差.

我们可以看下这个模型进行基数统计所需要的内存是多少:

• 能够统计对最多2 ^ 24 = 16777216个数据进行基数统计
• 总计2 ^ 6 = 64个桶
• 每个桶的Register Value对应的bit位取值范围是[0, 2 ^ 15), 即[0, 32767), 而Register Value本身的取值范围则是这一段bit的长度, 即[1, 15], 表示这个范围需要至少需要4个bit. 即每个桶需要的空间为4个bit.

所以需要的空间为64 * 4bit = 256bit = 32字节. 与之对比, Redis中使用HyperLogLog需要能对64位整形数据进行基数统计, 其中总共有2 ^ 16 = 16384个桶, 每个桶中需要6个bit来保存最大的Register Value, 所以需要占用内存为16384 * 6 / 8 = 12KB. 可以看到使用HLL来进行基数估计所需要的内存是非常少的.

Conclusion

了解了基数估计的基本思想, 就可以去尝试去看一些工业实现了, 除了Redis, Spark, Flink之外, 有一个专门来做大数据分析的开源项目中DataSketches, 它们的文档和代码风格都是比较不错的, 已经由Apache接受. 目前对接的也基本是Apache的项目, 比如Hive, Pig和Druid, 数据库方向主要接入了Postgre, 后续可以再了解下.

Reference

大数据领域的近似分析方法

基数估计算法

DataSketches